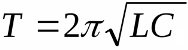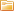Идеальный конденсатор и катушка. Как происходят колебания, куда движутся электроны, когда нарастает и исчезает магнитное поле катушки.
Колебательный контур — это замкнутая электрическая цепь, состоящая из катушки и конденсатора. Обозначим индуктивность катушки буквой L, а электроемкость конденсатора - буквой C. Колебательный контур — наиболее простая из электрических систем, в которой могут происходить свободные гармонические электромагнитные колебания.
Безусловно, реальный колебательный контур всегда включает в себя не только емкость С и индуктивность L, но еще и соединительные провода, непременно обладающие активным сопротивлением R, но давайте оставим сопротивление за рамками данной статьи, о нем вы сможете узнать в разделе о добротности колебательной системы. Итак, рассматриваем идеальный колебательный контур, и начнем с конденсатора.
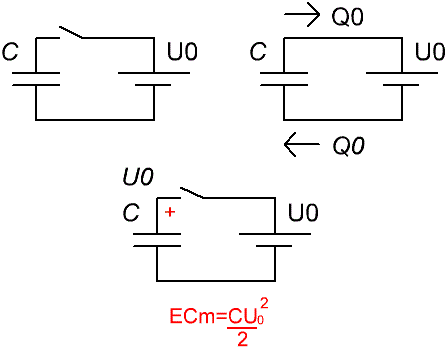
Допустим, есть идеальный конденсатор. Зарядим его от батарейки до напряжения U0, то есть создадим между его обкладками разность потенциалов U0, чтобы на верхней обкладке стал «+», а на нижней - «-», как это принято обозначать.
Что это значит? Это значит, что мы переместим, при помощи источника сторонних сил, некоторую порцию отрицательного заряда Q0 (состоящего из электронов), с верхней обкладки конденсатора — на нижнюю его обкладку. В итоге, на нижней обкладке конденсатора возникнет избыток отрицательного заряда, а на верхней — недостаток именно этого количества отрицательного заряда, а значит — избыток положительного. Ведь сначала то конденсатор был не заряжен, а значит заряда одинакового знака на обеих его обкладках было точно поровну.
Итак, конденсатор зарядился, верхняя обкладка зарядилась положительно (так как там недостает электронов) относительно нижней, а нижняя — отрицательно относительно верхней. В целом, для других объектов, конденсатор электрически нейтрален, однако внутри его диэлектрика существует электрическое поле, посредством которого противоположные заряды на противоположных обкладках взаимодействуют между собой, а именно — стремятся друг к другу притянуться, но диэлектрик, в силу своей природы, не дает этому произойти. В этот момент энергия конденсатора максимальна и равна ECm.
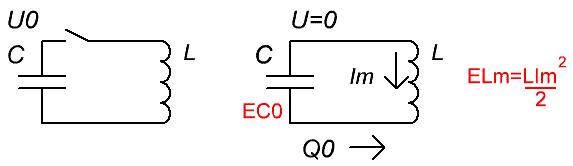Теперь возьмем идеальную катушку индуктивности. Путь она изготовлена из такого проводника, который вовсе не обладает электрическим сопротивлением, то есть имеет идеальную способность пропускать электрический заряд, не препятствуя ему. Соединим катушку параллельно с только что заряженным конденсатором.
Что произойдет? Заряды на обкладках конденсатора как и прежде взаимодействуют, стремятся друг к другу притянуться, - электроны с нижней обкладки стремятся попасть обратно на верхнюю, ведь оттуда их силой утащили на нижнюю, когда заряжали конденсатор. Система зарядов стремится вернутся к состоянию электрического равновесия, и тут присоединили катушку — проводник, скрученный в спираль, обладающий индуктивностью (способностью препятствовать изменению тока посредством магнитного поля, при прохождении этого тока возникающего)!
Электроны с нижней обкладки рванулись через провод катушки — к верхней обкладке конденсатора (можно сказать, что одновременно с этим положительный заряд устремился к нижней обкладке), но не могут мгновенно туда проскочить.
Почему? Потому что катушка обладает индуктивностью, а движущиеся через нее электроны — это уже ток, а раз ток — значит вокруг него должно быть магнитное поле. И вот, чем больше электронов входит в катушку — тем большим током они становятся, и тем большее магнитное поле вокруг катушки возникает.
Когда все электроны с нижней обкладки конденсатора окажутся внутри катушки — ток в ней будет максимальным Im, магнитное поле вокруг нее будет наибольшим, какое только способно создать это количество движущегося заряда будучи в ее проводе. В этот момент конденсатор полностью разряжен, энергия электрического поля в диэлектрике между его обкладками равно нулю EC0, но вся эта энергия сейчас заключена в магнитном поле катушки ELm.
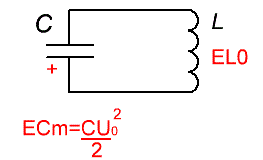
А дальше магнитное поле катушки начинает уменьшаться, ведь его ничему поддержать, так как других электронов в катушку не втекает и не вытекает, тока нет, и исчезающее вокруг катушки магнитное поле порождает в ее проводе вихревое электрическое поле, которое толкает электроны дальше — к верхней обкладке конденсатора, куда они так стремились. И в тот момент, когда все электроны оказались на верхней обкладке конденсатора, магнитное поле катушки стало равно нулю EL0. А конденсатор теперь заряжен противоположно по отношению к тому, как был заряжен в самом начале.
Верхняя обкладка конденсатора сейчас заряжена отрицательно, а нижняя - положительно. Катушка все еще подключена, ее провод по прежнему предоставляет свободный путь для движения электронов, а ведь разность потенциалов между обкладками конденсатора опять имеет место, хотя и противоположна по знаку изначальной.
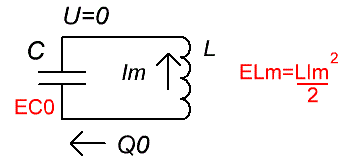И электроны снова устремляются в катушку, ток становится максимальным, но поскольку теперь он направлен в противоположном направлении, магнитное поле создается в противоположном направлении, и когда все электроны снова в катушке (в своем движении вниз), и магнитное поле больше не нарастает, теперь оно начинает уменьшаться, и электроны проталкиваются дальше - на нижнюю обкладку конденсатора.
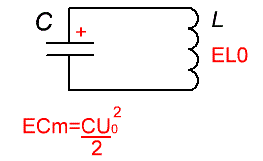
И в момент когда магнитное поле катушки стало равно нулю, исчезло полностью, - верхняя обкладка конденсатора вновь заряжена положительно относительно нижней. Состояние конденсатора стало аналогичным тому, что было в начале. Состоялся полный цикл из одного колебания. И так далее, и так далее.. Период этих колебаний, в зависимости от индуктивности катушки и от емкости конденсатора, может быть найден по формуле Томсона:
