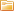Электромагнитные колебания в контуре, состоящем из катушки индуктивности и конденсатора, происходят благодаря периодическому превращению электрической энергии в магнитную и обратно. При этом периодически изменяются электрический заряд на обкладках конденсатора и величина тока через катушку.

Электромагнитные колебания бывают свободными и вынужденными. Свободные колебания, как правило, являются затухающими из-за ненулевого сопротивления контура, а вынужденные колебания — это, обычно, автоколебания.
Чтобы получить в колебательном контуре свободные колебания, необходимо сначала вывести данную систему из состояния равновесия: сообщить конденсатору начальный заряд q0, либо каким-то образом инициировать импульс тока I0 через катушку.
Это послужит своеобразным толчком, и свободные электромагнитные колебания возникнут в контуре - начнется процесс попеременной зарядки и разрядки конденсатора через катушку индуктивности и, соответственно, попеременного нарастания и спада магнитного поля катушки.
Колебания, которые поддерживаются в цепи под действием внешней переменной электродвижущей силы, называются вынужденными колебаниями. Итак, как вы уже поняли, примером простейшей колебательной системы, в которой можно наблюдать свободные электромагнитные колебания, является колебательный контур, состоящий из конденсатора электроемкостью C и катушки индуктивностью L.
В реальном колебательном контуре процесс перезарядки конденсатора периодически повторяется, но колебания быстро затухают, так как энергия рассеивается в основном на активном сопротивлении R провода катушки.
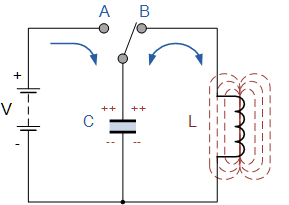
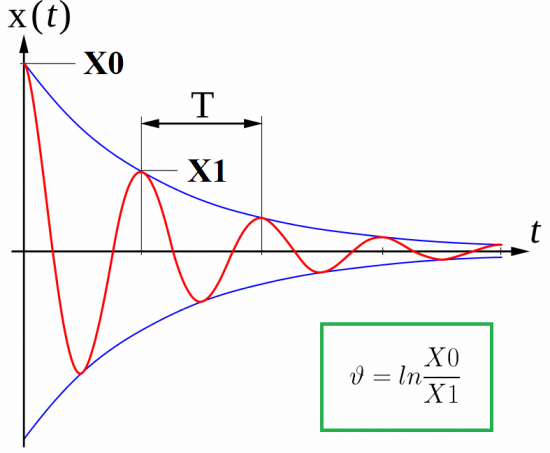
Рассмотрим схему с идеальным колебательным контуром. Зарядим сначала конденсатор от батареи — сообщим ему начальный заряд q0, то есть наполним конденсатор энергией. Это будет максимальная энергия конденсатора Wэ.
Следующим шагом отключим конденсатор от батареи и подключим его параллельно к катушке индуктивности. В этот момент конденсатор начнет разряжаться, и в цепи катушки возникнет нарастающий ток. Чем дольше разряжается конденсатор — тем больше заряда из него постепенно переходит в катушку, тем большим становится ток в катушке, катушка запасает таким образом энергию в форме магнитного поля.
Этот процесс происходит не мгновенно а постепенно, так как катушка обладает индуктивностью, а значит проявляется явление самоиндукции, которое заключается в том, что катушка как-бы противится нарастанию тока. В какой-то момент энергия магнитного поля катушки доходит до максимально возможного значения Wм (в зависимости от того, сколько заряда изначально было сообщено конденсатору и каково сопротивление цепи).
Далее, из-за явления самоиндукции, ток через катушку поддерживается в том же направлении, но величина его спадает, и электрический заряд в конце концов снова накапливается в конденсаторе. Конденсатор, таким образом, перезарядился. Его обкладки теперь имеют противоположные знаки заряда чем это было в начале эксперимента, когда мы подключали конденсатор к батарее.
Энергия конденсатора достигла максимально возможного для данной цепи значения. Ток в цепи прекратился. Теперь процесс начинает идти в обратном направлении. И так будет продолжаться вновь и вновь, то есть будут иметь место свободные электромагнитные колебания.
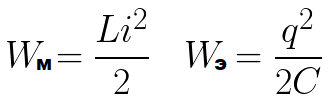
Если бы активное сопротивление цепи R было равно нулю, то напряжение на обкладках конденсатора и ток через катушку изменялись бы бесконечно по гармоническому закону — косинуса или синуса. Это и называется гармонические колебания. Заряд на обкладках конденсатора изменялся бы также по гармоническому закону.
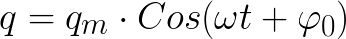
В идеальном контуре отсутствуют потери. И если бы так было на самом деле, то период свободных колебаний в контуре зависел бы лишь от величины емкости C конденсатора и индуктивности L катушки. Этот период можно найти (для идеального контура, у которого R=0) по формуле Томсона:
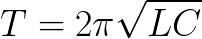
Соответствующие частота и циклическая частота находятся для идеального контура без потерь по следующим формулам:
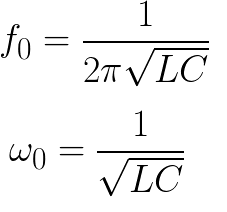
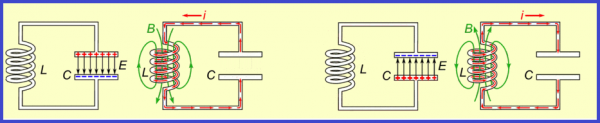
Но идеальных контуров не существует, и электромагнитные колебания затухают из-за потерь на нагрев проводов. В зависимости от величины сопротивления цепи контура R, каждый последующий максимум напряжения на конденсаторе будет ниже предыдущего.
В связи с данным явлением в физике вводится такой параметр как логарифмический декремент колебаний или декремент затухания. Он находится как натуральный логарифм отношения двух последующих максимумов (одного знака) колебаний:
Логарифмический декремент колебаний связан с идеальным периодом колебаний следующим соотношением, где может быть введен дополнительных параметр, так называемый коэффициент затухания:
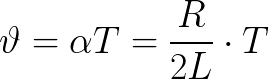
Затухание влияет на частоту свободных колебаний. Поэтому формула для нахождения частоты свободных затухающих колебаний в реальном колебательном контуре отличается от формулы для идеального контура (учитывается коэффициент затухания):
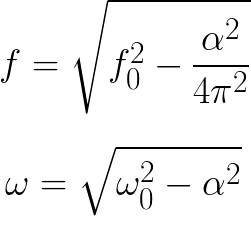
Чтобы колебания в контуре сделать незатухающими, необходимо эти потери каждые пол периода восполнять, компенсировать. Что и достигается в генераторах незатухающих колебаний, где источник внешней ЭДС компенсирует своей энергией тепловые потери. Такая система колебаний с источником внешней ЭДС называется автоколебательной.