В электрические цепи с конденсаторами входят источники электрической энергии и отдельные конденсаторы. Конденсатор представляет собой систему двух проводников любой формы, разделенных слоем диэлектрика. Присоединение зажимов конденсатора к источнику электрической энергии с постоянным напряжением U сопровождается накоплением на одной из его пластин заряда +Q, а на другой -Q.
В электрические цепи с конденсаторами входят источники электрической энергии и отдельные конденсаторы. Конденсатор представляет собой систему двух проводников любой формы, разделенных слоем диэлектрика. Присоединение зажимов конденсатора к источнику электрической энергии с постоянным напряжением U сопровождается накоплением на одной из его пластин заряда +Q, а на другой -Q.
Величина этих зарядов прямо пропорциональна напряжению U и определяется по формуле
Q=C∙U,
где C – емкость конденсатора, измеряемая в фарадах (Ф).
Величина емкости конденсатора равна отношению заряда одной из его пластин к напряжению между ними, т. е. C=Q/U,
Емкость конденсатора зависит от формы пластин, их размеров, взаимного расположения, а также от диэлектрической проницаемости среды между пластинами.
Емкость плоского конденсатора, выраженная в микрофарадах, определяется по формуле
C=((ε0∙εr∙S)/d)∙106,
где ε0 – абсолютная диэлектрическая проницаемость вакуума, εr – относительная диэлектрическая проницаемость среды между пластинами, S – площадь пластины, м2, d – расстояние между пластинами, м.
Абсолютная диэлектрическая проницаемость вакуума является постоянной величиной ε0=8,855∙10-12 Ф⁄м.
Величина напряженности электрического поля E между пластинами плоского конденсатора, находящимися под напряжением U, определяется по формуле E=U/d .
В Международной системе единиц измерения (СИ) единицей измерения напряженности электрического поля является вольт на метр (В⁄м).
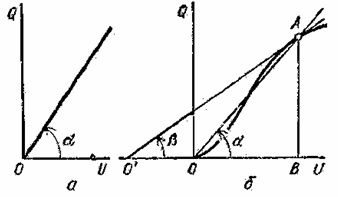
Рис. 1. Кулон-вольтные характеристики конденсатора: а – линейная, б – нелинейная
Если относительная диэлектрическая проницаемость среды, находящейся между пластинами конденсатора, не зависит от величины напряженности электрического поля, то емкость конденсатора не зависит от величины напряжения на его зажимах и кулон-вольтная характеристика Q=F(U) линейна (рис. 1, а).
Конденсаторы с диэлектриком из сегнетоэлектриков, у которых относительная диэлектрическая проницаемость зависит от напряженности электрического поля, имеют нелинейную кулон-вольтную характеристику (рис. 1, б).
У таких нелинейных конденсаторов, или варикондов, каждой точке кулон-вольтной характеристики, например точке А, соответствует статическая емкость Cст=Q/U=(mQ∙BA)/(mU∙OB)=mC∙tanα и дифференциальная емкость Cдиф=dQ/dU=(mQ∙BA)/(mU∙O'B)=mC∙tanβ, где mC – коэффициент, зависящий от масштабов mQ и mU, принятых соответственно для зарядов и напряжений.
Каждый конденсатор характеризуется не только величиной емкости, но и величиной рабочего напряжения Uраб, которая принимается так, чтобы возникающая при этом напряженность электрического поля была меньше электрической прочности диэлектрика. Электрическая прочность диэлектрика определяется наименьшим значением напряженности, при которой начинается пробой диэлектрика, сопровождаемый его разрушением и потерей изоляционных свойств.
Диэлектрики характеризуются не только электрической прочностью, но и очень большим объемным сопротивлением ρV, составляющим примерно от 1010 до 1020 Ом•см, в то время как у металлов оно от 10-6 до 10-4 Ом•см.
Кроме того, для диэлектриков вводят еще понятие удельного поверхностного сопротивления ρS, характеризующего их противодействие току утечки по поверхности. У некоторых диэлектриков эта величина незначительна и поэтому они не пробиваются, а перекрываются электрическим разрядом по поверхности.
Для расчета величины напряжений на зажимах отдельных конденсаторов, входящих в многоконтурные электрические цепи, при заданных э.д.с. источников электрической энергии пользуются уравнениями, аналогичными уравнениям законов Кирхгофа для электрических цепей постоянного тока.
Так, для любого узла многоконтурной электрической цепи с конденсаторами оправдывается закон сохранения количества электричества ∑Q=Q0, который устанавливает, что алгебраическая сумма зарядов на пластинах конденсаторов, присоединенных к одному узлу, равна алгебраической сумме зарядов, которые были до их соединения между собой. Это же уравнение при отсутствии предварительных зарядов на пластинах конденсаторов имеет вид ∑Q=0.
Для любого контура электрической цепи с конденсаторами справедливо равенство ∑E=∑Q/C, которое утверждает, что алгебраическая сумма э.д.с. в контуре равна алгебраической сумме напряжений на зажимах конденсаторов, входящих в данной контур.
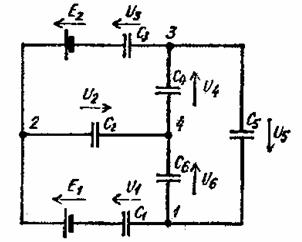
Рис. 2. Многоконтурная электрическая цепь с конденсаторами
Так, в много контурной электрической цепи с двумя источниками электрической энергии и шестью конденсаторами при начальных нулевых зарядах и произвольно выбранных положительных направлениях напряжений U1, U2, U3, U4, U5, U6 (рис. 2) на основании закона сохранения количества электричества для трех независимых узлов 1, 2, 3 получаем три уравнения: Q1+Q6-Q5=0, -Q1-Q2-Q3=0, Q3-Q4+Q5=0.
Дополнительные уравнения к трем независимым контурам 1—2—4—1, 2—3—4—2, 1—4—3—1 при обходе их по направлению движения стрелки часов имеют вид E1=Q1/C1 +Q2/C2 -Q6/C6 , -E2=-Q3/C3 -Q4/C4 -Q2/C2 , 0= Q6/C6 +Q4/C4 +Q5/C5 .
Решение системы из шести линейных уравнений позволяет определить величину заряда каждого конденсатора Qi и найти напряжение на его зажимах Ui по формуле Ui=Qi/Ci .
Истинные направления напряжений Ui, численные значения которых получены со знаком минус, противоположны первоначально принятым при составлении уравнений.
При расчете многоконтурной электрической цепи с конденсаторами иногда полезно конденсаторы C12, C23, C31, соединенные треугольником, заменить конденсаторами C1, C2, C3, соединенными эквивалентной трехлучевой звездой.
В этом случае искомые емкости находят так: C1=C12+C31+(C12∙C31)/C23 , C2=C23+C12+(C23∙C12)/C31 , C3=C31+C23+(C31∙C23)/C12 .
При обратном преобразовании пользуются формулами: C12=(C1∙C2)/(C1+C2+C3 ), C23=(C2∙C3)/(C1+C2+C3 ), C31=(C3∙C1)/(C1+C2+C3 ).
Конденсаторы емкостью C1, C2, …, Cn, соединенные параллельно, можно заменить одним конденсатором емкостью
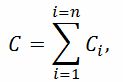
а при последовательном их соединении – конденсатором, емкость которого
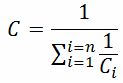
Если конденсаторы, входящие в электрическую цепь, имеют диэлектрики с заметными электрическими проводимостями, то в такой цепи возникают небольшие токи, величины которых определяют обычными методами, принятыми при расчете электрических цепей постоянного тока, а напряжения на зажимах каждого конденсатора при установившемся режиме находят по формуле
Ui=Ri∙Ii,
где Ri – электрическое сопротивление диэлектрического слоя i-го конденсатора, Ii – ток этого же конденсатора.
Смотрите по этой теме: Заряд и разряд конденсатора