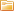Рассматривая цепь переменного тока, содержащую только индуктивное сопротивление (смотрите статью "Катушка индуктивности в цепи переменного тока"), мы предполагали равным нулю активное сопротивление этой цепи.
Однако в действительности как провод самой катушки, так и соединительные провода обладают хотя и небольшим, но активным сопротивлением, поэтому цепь неизбежно потребляет энергию источника тока.
Поэтому при определении общего сопротивления внешней цепи нужно складывать ее реактивное и активное сопротивления. Но складывать эти два различных по своему характеру сопротивления нельзя.
В этом случае полное сопротивление цепи переменному току находят путем геометрического сложения.
Строят прямоугольный треугольник (см. рисунок 1) одной стороной которого служит величина индуктивного сопротивления, а другой - величина активного сопротивления. Искомое полное сопротивление цепи определится третьей стороной треугольника.

Рисунок 1. Определение полного сопротивления цепи, содержащей индуктивное и активное сопротивление
Полное сопротивление цепи обозначается латинской буквой Z и измеряется в омах. Из построения видно, что полное сопротивление всегда больше индуктивного и активного сопротивлений, отдельно взятых.
Алгебраическое выражение полного сопротивления цепи имеет вид:
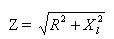
где Z — общее сопротивление, R — активное сопротивление, XL — индуктивное сопротивление цепи.
Таким образом, полное сопротивление цепи переменному току, состоящей из активного и индуктивною сопротивлений, равно корню квадратному из суммы квадратов активного и индуктивного сопротивлений этой цепи.
Закон Ома для такой цепи выразится формулой I = U / Z,где Z — общее сопротивление цепи.
Разберем теперь, какое будет напряжение, если цепь, кроме и и сдвиг фаз между током и на индуктивности, обладает также сравнительно большим активным сопротивлением. На практике такой цепью может служить, например, цепь, содержащая катушку индуктивности без железного сердечника, намотанную из тонкой проволоки (дроссель высокой частоты).
В этом случае сдвиг фаз между током и напряжением составит уже не четверть периода (как это было в цепи только с индуктивным сопротивлением), а значительно меньше; причем чем больше будет активное сопротивление, тем меньший получится сдвиг фаз.
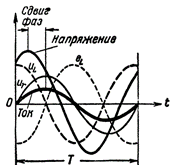
Рисунок 2. Ток и напряжение в цепи, содержащей R и L
Теперь и сама ЭДС самоиндукции не находится в противофазе с напряжением источника тока, так как сдвинута относительно напряжения уже не на половину периода, а меньше. Кроме того, напряжение, создаваемое источником тока на зажимах катушки, не равно ЭДС самоиндукции, а больше нее на величину падения напряжения в активном сопротивлении провода катушки. Иначе говоря, напряжение на катушке состоит как бы из двух слагающих:
-
uL— реактивной слагающей напряжения, уравновешивающей действие ЭДС самоиндукции,
-
uR— активной слагающей напряжения, идущей на преодоление активного сопротивления цепи.
Если бы мы включили в цепь последовательно с катушкой большое активное сопротивление, то сдвиг фаз настолько бы уменьшился, что синусоида тока почти догнала бы синусоиду напряжения и разность фаз между ними была бы едва заметна. В этом случае амплитуда слагающей и, была бы больше амплитуды слагающей.
Точно так же можно уменьшить сдвиг фаз и даже совсем свести его к нулю, если уменьшить каким-либо способом частоте генератора. Уменьшение частоты приведет к уменьшению ЭДС самоиндукции, а следовательно, и к уменьшению вызываемого ею сдвига фаз между током и напряжением в цепи.

Мощность цепи переменного тока, содержащей катушку индуктивности
Цепь переменного тока, содержащая катушку, не потребляет энергии источника тока и что в цепи происходит процесс обмена энергией между генератором и цепью.
Разберем теперь, как будет обстоять дело с мощностью, потребляемой такой цепью.
Мощность, потребляемая в цепи переменного тока, равна произведению тока на напряжение, но так как ток и напряжение есть переменные величины, то и мощность будет также переменной. При этом значение мощности для каждого момента времени мы сможем определить, если умножим величину тока на величину напряжения, соответствующую данному моменту времени.
При построении этой кривой использовалось следующее правило алгебраического умножения: при умножении положительной величины на отрицательную получается отрицательная величина, а при перемножении двух отрицательных или двух положительных — положительная величина.
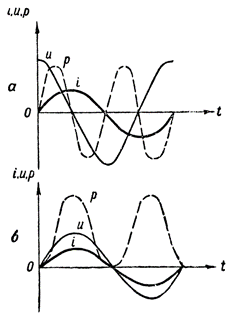
Рисунок 3. Графики мощности: а - в цепи содержащей индуктивное сопротивление, б - тоже, активное сопротивление
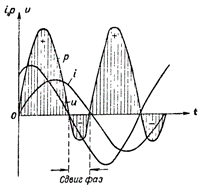
Рисунок 4. График мощности для цепи, содержащей R и L
Кривая мощности в этом случае расположена выше оси времени. Это значит, что обмена энергией между генератором и цепью не происходит, а следовательно, мощность, отдаваемая генератором в цепь, полностью потребляется цепью.
На рис. 4 изображен график мощности для цепи, содержащей в себе одновременно индуктивное и активное сопротивления. В этом случае также происходит обратный переход энергии из цепи к источнику тока, однако в значительно меньшей степени, чем в цепи с одним индуктивным сопротивлением.
Рассмотрев приведенные выше графики мощности, мы приходим к выводу, что только сдвиг фаз между током и напряжением в цепи создает "отрицательную" мощность. При этом, чем больше будет сдвиг фаз между током и напряжением в цепи тем потребляемая цепью мощность будет меньше, и, наоборот, чем меньше сдвиг фаз, тем потребляемая цепью мощность будет больше.
Читайте также: Что такое резонанс напряжений