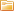В процессе расчетов электрических цепей переменного синусоидального тока часто бывает полезен Закон Ома в комплексной форме. Под электрической цепью здесь понимается линейная цепь в установившемся режиме работы, то есть такая цепь, в которой переходные процессы завершились и токи установились.
Падения напряжений, ЭДС источников и токи в ветвях такой цепи являются попросту тригонометрическими функциями времени. Ежели даже в установившемся режиме форма тока в цепи не является синусоидой (меандр, пила, импульсные помехи), то и Закон Ома в комплексной форме будет уже не применим.
Так или иначе, всюду в промышленности сегодня применяется система трехфазного переменного синусоидального тока. Напряжение в таких сетях имеет строго определенные частоту и действующее значение. Именно по этой причине, по причине столь явной унификации, Закон Ома в комплексной форме и удобен во многих расчетах электрических цепей (где он применяется совместно с Правилами Кирхгофа).
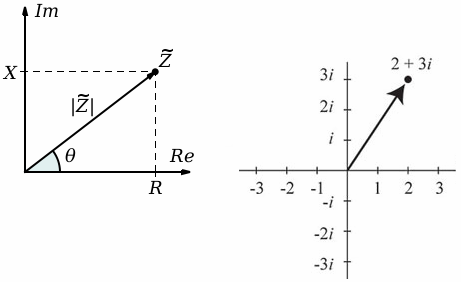
Обычная форма записи Закона Ома отличается от комплексной формы его записи. В комплексной форме обозначения ЭДС, напряжений, токов, сопротивлений, - записываются как комплексные числа. Это необходимо для того, чтобы удобно учитывать и вести расчеты как с активными, так и с реактивными сопротивлениями, имеющими место в цепях переменного тока.
Не всегда можно просто взять и поделить падение напряжения на ток, иногда важно учесть характер участка цепи, и это вынуждает нас вносить в математику определенные дополнения.
Символьный метод (метод с комплексными числами) позволяет избавиться от надобности решать дифференциальные уравнения в процессе расчета электрической цепи синусоидального тока. Ибо в цепи переменного тока бывает такое, что ток например есть, а падения напряжения на участке цепи нет; или падение напряжения есть, а тока в цепи нет, в то время как цепь, казалось бы, замкнута.
В цепях постоянного тока такое просто невозможно. Вот почему для переменного тока и Закон Ома отличается. Разве что для чисто активной нагрузки в однофазной цепи он может применяться почти без отличий от расчетов с током постоянным.

Комплексное число состоит из мнимой Im и вещественной Re части, при этом его можно представить вектором в полярных координатах. Для вектора будет характерен некий модуль и угол, на который он повернут вокруг начала координат относительно оси абсцисс. Модуль есть амплитуда, а угол — начальная фаза.
Запись данного вектора можно произвести в тригонометрической, показательной или алгебраической формах. Это и будет символьное изображение реальных физических явлений, ибо в реальности мнимых и вещественных характеристик в цепях на самом деле нет. Это лишь удобный метод решения электротехнических задач с цепями.
Комплексные числа можно делить, умножать, складывать, возводить в степень. Эти операции необходимо уметь выполнять чтобы мочь применять Закон Ома в комплексной форме.
Сопротивления в цепях переменного тока подразделяют на: активное, реактивное и полное. Кроме того следует отличать проводимость. Электроемкость и индуктивность обладают реактивными сопротивлениями переменному току. Реактивные сопротивления относятся к мнимой части, а активное сопротивление и проводимость — к части вещественной, то есть к вполне реальной.
Запись сопротивлений в символической форме несет за собой определенный физический смысл. На активном сопротивлении электроэнергия реально рассеивается в форме тепла по Закону Джоуля-Ленца, в то время как на емкости и индуктивности она преобразуется в энергию электрического и магнитного полей. И возможны преобразования энергии из одной из этих форм - в другую: из энергии магнитного поля — в тепловую или из энергии электрического поля частично в магнитную, а частично — в тепловую и т. д.

Традиционно токи, падения напряжений и ЭДС записывают в тригонометрическом виде, где учитываются как амплитуда, так и фаза, что вполне явно отражает физический смысл явления. Однако угловая частота у напряжений и токов может отличаться, поэтому практически более удобна алгебраическая форма записи.
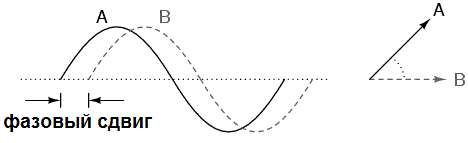
Наличие угла между током и напряжением приводит к тому, что во время колебаний существуют такие моменты, когда ток (или падение напряжения) равен нулю, а падение напряжения (или ток) не равно нулю. Когда напряжение и ток находятся в одной фазе, то угол между ними кратен 180°, и тогда если падение напряжения равно нулю, то и ток в цепи равен нулю. Речь о мгновенных значениях.
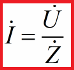
Итак, понимая алгебраическую запись, можно записать теперь Закон Ома в комплексной форме. Вместо активного сопротивления (свойственного цепям постоянного тока) здесь будет записываться полное (комплексное) сопротивление Z, а действующие значения ЭДС, токов и напряжений — станут комплексными величинами.
Во время расчета электрической цепи с применением комплексных чисел, важно помнить, что данный метод применим только к цепям синусоидального тока и именно в установившемся режиме работы.
Андрей Повный