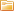Несинусоидальные токи и их разложение
В электрической цепи несинусоидальные токи могут возникнуть по двум причинам:
-
сама электрическая цепь является линейной, но на цепь действует несинусоидальное напряжение,
-
воздействующее на цепь напряжение является синусоидальным, но электрическая цепь содержит нелинейные элементы.
Может иметь место также наличие обеих указанных причин. В данной главе рассматриваются цепи только по первому пункту. При этом считается, что несинусоидальные напряжения являются периодическими.
Генераторы периодических импульсов применяются в различных устройствах радиотехники, автоматики, телемеханики. Форма импульсов может быть различной: пилообразной, ступенчатой, прямоугольной (рис. 1).
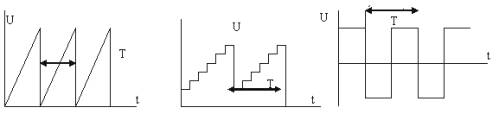
Рисунок 1. Формы импульсов
Явления, происходящие в линейной электрической цепи при периодических, но несинусоидальных напряжениях, проще всего поддаются исследованию, если кривую напряжения разложить в тригонометрический ряд Фурье:
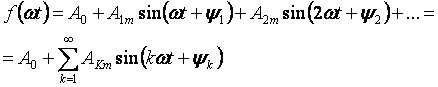
Первый член ряда А0 называется постоянной составляющей или нулевой гармоникой, второй член ряда
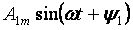
- основной или первой гармоникой, а все остальные члены вида
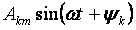
при к>1 носят название высших гармоник.
Если в выражении (3.1) раскрыть синус суммы, то можно перейти и к другой форме записи ряда:
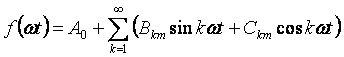
Некоторые примеры разложения в ряд приведены в табл. 1, а также они имеются в справочной литературе.
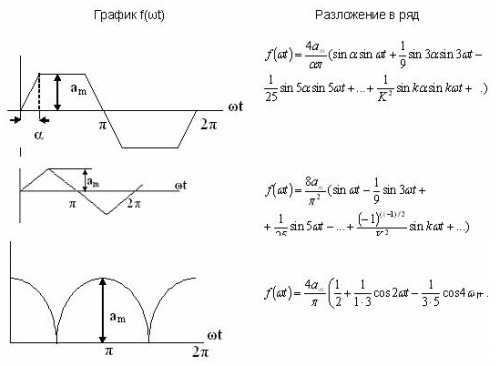
Таблица 1. Разложение в ряд Фурье
Расчет цепей несинусоидального тока
Расчет цепи производится для каждой гармоники по модельности. Цепь рассчитывается столько раз, сколько гармоник содержит воздействующее на цепь напряжение. При этом необходимо учитывать ряд особенностей.
Надо иметь в виду, что сопротивление индуктивного элемента возрастает с ростом номера гармоники
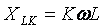
а емкостного элемента напротив уменьшается:
Также надо учитывать, что постоянная составляющая тока не проходит через емкость, а индуктивность не представляет для нее сопротивление.
Кроме того, следует не забывать возможные резонансные явления не только на основной гармонике, но и на высших гармониках.
Векторные диаграммы можно строить для каждой гармоники отдельно.
Согласно принципу наложения ток любой ветви может состоять из суммы отдельных слагаемых (нулевой, основной и высших гармоник):
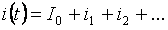
Действующие значение полного тока ветви может быть определено через действующее значение токов отдельных гармоник:
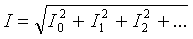
Активная мощность несинусоидального тока равна сумме активных мощностей отдельных гармоник:
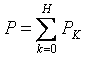
Ниже приводится в общем виде пример расчета цепей несинусоидального тока. Все токи, напряжения, сопротивления будут иметь два индекса: первая цифра означает номер ветви, а вторая цифра – номер гармоники. Входное напряжение:
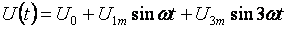
- Постоянная составляющая
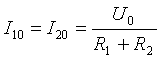
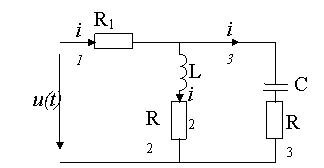
Рисунок 2. Схема цепи
- Основная гармоника:
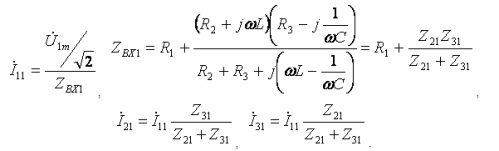
- Третья гармоника:
