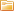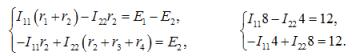Метод контурных токов используется для расчета резистивных линейных
цепей с постоянными токами и для расчета комплексных схем замещения линейных
цепей с гармоническими токами. При этом в расчет вводятся контурные токи – это
фиктивные токи, которые замыкаются в независимых замкнутых контурах,
отличающихся друг от друга наличием хотя бы одной новой ветви.
Методика расчета цепи методом контурных токов
В методе контурных токов за неизвестные величины принимаются расчетные (контурные) токи, которые якобы протекают в каждом из независимых контуров. Таким образом, количество неизвестных токов и уравнений в системе равно числу независимых контуров цепи.
Расчет токов ветвей по методу контурных токов выполняют в следующем порядке:
1 Вычерчиваем принципиальную схему цепи и обозначаем все элементы.
2 Определяем все независимые контуры.
3 Произвольно задаемся направлением протекания контурных токов в каждом из независимых контуров (по часовой стрелке или против). Обозначаем эти токи. Для нумерации контурных токов можно использовать арабские сдвоенные цифры (I11, I22, I33 и т. д.) или римские цифры.
4 По второму закону Кирхгофа, относительно контурных токов, составляем уравнения для всех независимых контуров. При записи равенства считать, что направление обхода контура, для которого составляется уравнение, совпадает с направлением контурного тока данного контура. Следует учитывать и тот факт, что в смежных ветвях, принадлежащих двум контурам, протекают два контурных тока. Падение напряжения на потребителях в таких ветвях надо брать от каждого тока в отдельности.
5 Решаем любым методом полученную систему относительно контурных токов и определяем их.
6 Произвольно задаемся направлением реальных токов всех ветвей и обозначаем их. Маркировать реальные токи надо таким образом, чтобы не путать с контурными. Для нумерации реальных токов можно использовать одиночные арабские цифры (I1, I2, I3 и т. д.).
7 Переходим от контурных токов к реальным, считая, что реальный ток ветви равен алгебраической сумме контурных токов, протекающих по данной ветви.
При алгебраическом суммировании без изменения знака берется контурный ток, направление которого совпадает с принятым направлением реального тока ветви. В противном случае контурный ток умножается на минус единицу.
Пример расчёта сложной цепи методом контурных токов
В цепи, изображённой на рисунке 1, рассчитать все токи методом контурных токов. Параметры цепи: Е1 = 24 В, Е2 = 12 В, r1 = r2 = 4 Ом, r3 = 1 Ом, r4 = 3 Ом.
Рис. 1. Схема электрической цепи для примера расчета по методу контурных токов
Решение. Для расчета сложной цепи этим методом достаточно составить два уравнения, по числу независимых контуров. Контурные токи направляем по часовой стрелке и обозначаем I11 и I22 (см. рисунок 1).
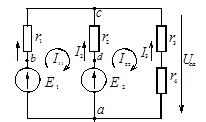
По второму закону Кирхгофа относительно контурных токов составляем уравнения:
Решаем систему и получаем контурные токи I11 = I22 = 3 А.
Произвольно задаемся направлением реальных токов всех ветвей и обозначаем их. На рисунке 1 такими токами являются I1, I2, I3. Направление у этих токов одинаковое – вертикально вверх.
Переходим от контурных токов к реальным. В первой ветви протекает только один контурный ток I11. Направление его совпадает с направлением реального тока ветви. В таком случае реальный ток I1 + I11 = 3 А.
Реальный ток второй ветви формируется двумя контурными I11 и I22. Ток I22 совпадает по направлению с реальным, а I11 направлен навстречу реальному. В результате I2 = I22 - I11 = 3 - 3 = 0А.
В третьей ветви протекает только контурный ток I22. Направление этого тока противоположно направлению реального, поэтому для I3 можно записать I3 = -I22 = -3А.
Следует отметить, как положительный факт, что в методе контурных токов по сравнению с решением по законам Кихгофа приходится решать систему уравнений меньшего порядка. Однако этот метод не позволяет сразу определять реальные токи ветвей.