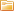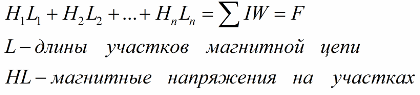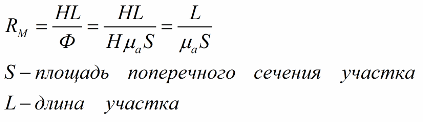Для некоторых технических целей, пример пары из них мы здесь рассмотрим, требуется рассчитывать параметры магнитных цепей. И главным инструментом в этих расчетах служит закон полного тока. Он звучит так: линейный интеграл вектора напряженности магнитного поля по замкнутому контуру равен алгебраической сумме токов, этим контуром охватываемых. Закон полного тока записывается так:
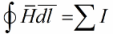
А если при этом контур интегрирования охватывает катушку из W витков, по которой течет ток I, то алгебраическая сумма токов есть произведение I*W – это произведение называется магнитодвижущей силой МДС, которая обозначается F. Данное положение запишем так:
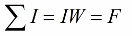
Контур интегрирования зачастую выбирают таким, что он совпадает с силовой линией магнитного поля, в этом случае векторное произведение заменяется на обычное произведение скалярных величин, интеграл заменяют суммой произведений H*L, далее выбирают участки магнитной цепи так, чтобы напряженности H вдоль них можно было бы считать постоянными. Тогда закон полного тока принимает более простой вид:
Здесь, кстати, вводят понятие «магнитное сопротивление», определяемое как отношение магнитного напряжения H*L на данном участке к магнитному потоку Ф на нем:
Для примера рассмотрим магнитную цепь, изображенную на рисунке. Здесь ферромагнитный сердечник имеет по всей своей длине одну и ту же площадь поперечного сечения S. Имеет определенную длину средней силовой лини магнитного поля L, а также воздушный зазор известной величины сигма. По обмотке, намотанной на данный магнитопровод, течет определенный намагничивающий ток I.
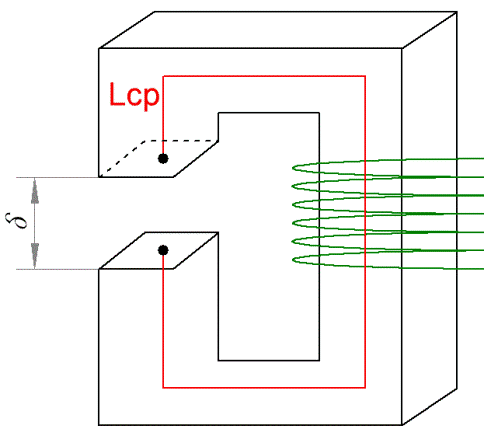
В прямой задаче по расчету магнитной цепи, исходя из заданного магнитного потока Ф в магнитопроводе, находят величину МДС F. Сначала определяют индукцию B в магнитопроводе, для этого делят магнитный поток Ф на площадь сечения S магнитопровода.
Вторым шагом по кривой намагничивания находят величину напряженности H магнитного поля, соответствующую данной величине индукции B. Затем записывают закон полного тока, в который включают все участки магнитной цепи:
Пример прямой задачи
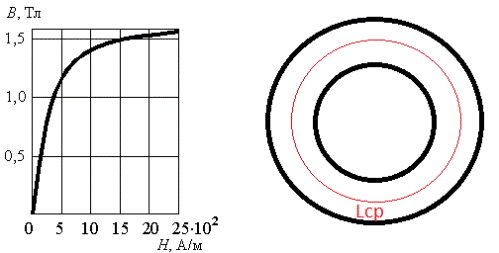
Допустим, есть замкнутый магнитопровод — тороидальный сердечник из трансформаторной стали, индукция насыщения в нем составляет 1,7 Тл. Необходимо найти ток намагничивания I, при котором сердечник войдет в насыщение, если известно, что обмотка содержит W=1000 витков. Длина средней линии равна Lср = 0,5 м. Дана кривая намагничивания.
Решение:
H*Lср=W*I.
Находим H по кривой намагничивания: H=2500А/м.
Следовательно I=H*Lср/W=2500*0,5/1000=1,25 (ампер).
Примечание. Аналогичным образом решаются задачи с немагнитным зазором, тогда в левой части уравнения будет сумма всех HL для участков магнитопровода и для участка зазора. Напряженность магнитного поля в зазоре находится делением магнитного потока (по магнитной цепи он везде один и тот же) на площадь зазора и на магнитную проницаемость в зазоре.
Обратная задача по расчету магнитной цепи предполагает, что исходя из известной магнитодвижущей силы F необходимо найти величину магнитного потока.
Для решения этой задачи иногда прибегают к магнитной характеристике цепи МДС F = f(Ф), где нескольким значениям магнитного потока Ф соответствует каждому свое значение МДС F. Так исходя из F можно найти значение магнитного потока Ф.
Пример обратной задачи
На замкнутый тороидальный магнитопровод (как в предыдущей прямой задаче) из трансформаторной стали намотана обмотка из W=1000 витков, по обмотке течет ток I=1,25 ампер. Длина средней линии равна L=0,5 м. Сечение магнитопровода S = 35 кв.см. Найти магнитный поток Ф в сердечнике, пользуясь приведенной кривой намагниченности.
Решение:
МДС F=I*W=1,25*1000=1250 ампер-виток. F=HL, значит H=F/L=1250/0,5=2500А/м.
По кривой намагничивания находим, что при данной напряженности индукция составляет B = 1,7 Тл.
Магнитный поток Ф=B*S, значит Ф=1,7*0,0035=0,00595 Вб.
Примечание. Магнитный поток по всей неразветвленной магнитной цепи будет одинаковым, и даже если есть воздушный зазор, то в нем магнитный поток будет тем же, подобно току в электрической цепи. См. Закон Ома для магнитной цепи.
Другие примеры: Расчет магнитных цепей
Андрей Повный