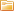В обычной жизни человека слова «потери» и «падение» применяются для обозначения факта снижения определенных достижений, но обозначают разную величину.
В обычной жизни человека слова «потери» и «падение» применяются для обозначения факта снижения определенных достижений, но обозначают разную величину.
При этом «потерями» обозначает утрату части, ущерб, уменьшение количества достигнутого ранее уровня. Потери нежелательны, но с ними можно мириться.
Под словом «падение» понимается более серьёзный урон, связанный с полным лишением прав. Таким образом, даже иногда происходящие потери (скажем, кошелька) со временем могут привести к падению (например, уровня материальной жизни).
В этом плане рассмотрим этот вопрос по отношению к напряжению электрической сети.
Как образуется потери и падение напряжения
Электроэнергия на большие расстояния передается по воздушным линиям от одной подстанции к другой.
Провода ВЛ рассчитаны на передачу допустимой мощности и изготавливаются из металлических жил определенного материала и сечения. Они создают активную нагрузку с величиной сопротивления R и реактивную — X.
На приемной стороне стоит трансформатор, преобразующий электроэнергию. Его обмотки обладают активным и ярко выраженным индуктивным сопротивлением XL. Вторичная сторона трансформатора понижает напряжение и передает его дальше потребителям, нагрузка которых выражается величиной Z и носит активный, емкостной и индуктивный характер. Она тоже оказывает влияние на электрические параметры сети.
Напряжение, приложенное на провода ближайшей к передающей электроэнергию подстанции опоре ВЛ, преодолевает реактивное и активное сопротивление цепи в каждой фазе и создает в ней ток, вектор которого отклоняется от вектора приложенного напряжения на угол φ.
Характер распределения напряжений и протекания токов по линии для симметричного режима нагрузки показан на картинке.
Поскольку каждая фаза линии питает разное количество потребителей, которые к тому же случайным порядком отключаются или подключаются в работу, то идеально сбалансировать фазную нагрузку технически очень сложно. В ней всегда есть небаланс, который определяется векторным сложением токов фаз и записывается величиной 3I0. В большинстве расчетов им просто пренебрегают.
Энергия, затраченная передающей подстанцией, частично расходуется на преодоление сопротивления линии и доходит до приемной стороны с небольшими изменениями. Эта доля характеризуется потерей и падением напряжения, вектор которого немного уменьшается по амплитуде и сдвигается по углу в каждой фазе.
Как рассчитываются потери и падение напряжения
Для понимания процессов, происходящих при передаче электроэнергии, удобна векторная форма представления основных характеристик. Различные математические методы расчета также базируются на этом способе.
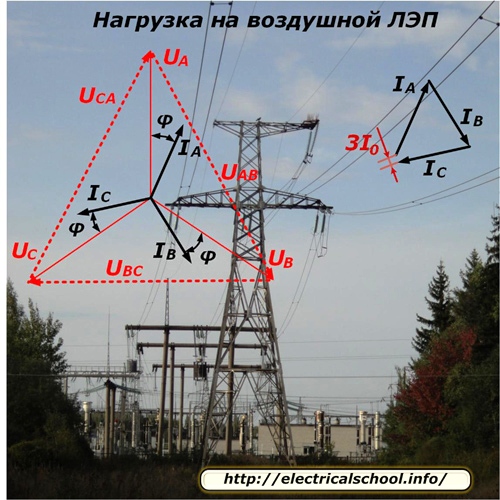
Чтобы упростить вычисления в трехфазной системе ее представляют тремя однофазными схемами замещения. Этот способ хорошо работает при симметричной нагрузке и позволяет анализировать процессы при ее нарушениях.
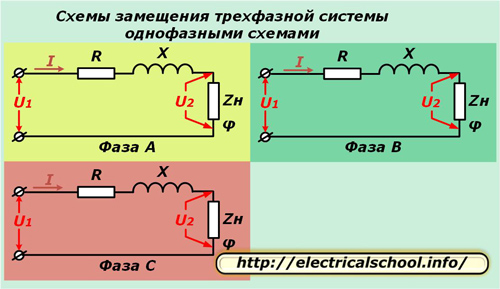
В приведенных схемах активное R и реактивное X сопротивление каждого провода линии подключаются последовательно к комплексному сопротивлению нагрузки Zн, характеризуемой углом φ.
Далее проводится расчет потери и падения напряжения в одной фазе. Для этого надо задать данные. С этой целью выбирается подстанция, принимающая энергию, на которой уже должна быть определена допустимая нагрузка.
Величина напряжения каждой высоковольтной системы уже задана справочниками, а сопротивления проводов определяются по их длине, поперечному сечению, материалу и конфигурации сети. Максимальный ток в цепи задан и ограничен свойствами проводников.
Поэтому для начала вычислений мы имеем: U2, R, X, Z, I, φ.
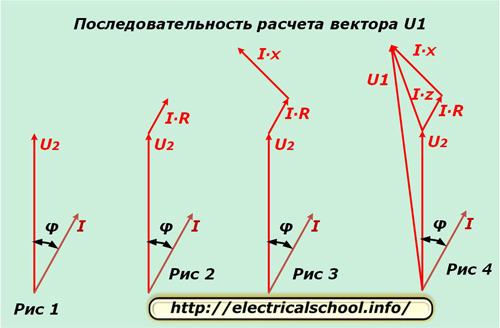
Берем одну фазу, например, «А» и откладываем для нее на комплексной плоскости вектора U2 и I, сдвинутые на угол φ, как показано на рисунке 1. Разность потенциалов на активном сопротивлении провода совпадает по направлению с током, а по величине определяется выражением I∙R. Этот вектор откладываем от окончания U2 (Рис. 2).
Разность потенциалов на реактивном сопротивлении провода отличается от направления тока на угол φ1 и вычисляется произведением I∙X. Откладываем его от вектора I∙R (Рис. 3).
Напоминания: за положительное направления вращения векторов на комплексной плоскости принято движение, противоположное ходу часовой стрелки. Ток, проходящий через индуктивную нагрузку, отстает по углу от приложенного напряжения.
На рисунке 4 показано вычерчивание векторов разности потенциалов на общем сопротивлении провода I∙Z и напряжения на входе в схему U1.
Теперь можно сравнивать вектора на входе в схему замещения и на нагрузке. Для этого расположим полученную диаграмму горизонтально (Рис. 5) и из начала координат проведем дугу с радиусом модуля U1 до пересечения с направлением вектора U2 (Рис. 6).
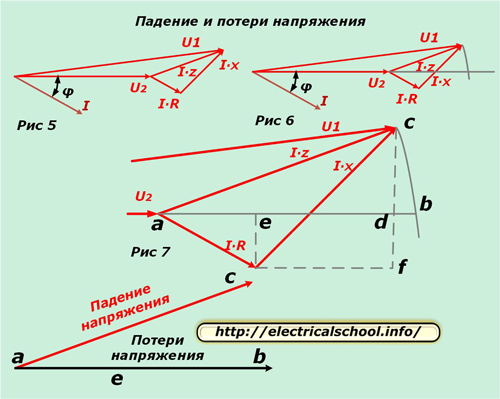
На рисунке 7 показано увеличение треугольника для наглядности и проведение вспомогательных линий, обозначение характерных точек пересечения буквами.
Внизу картинки показано, что получившийся вектор ac называют падением напряжения, а ab — потерями. Они отличаются по величине и направлению. Если вернуться к исходному масштабу, то будет видно, что ас получен в результате геометрического вычитания векторов (U2 из U1), а ab — арифметического. Этот процесс показан на картинке ниже (Рис. 8).
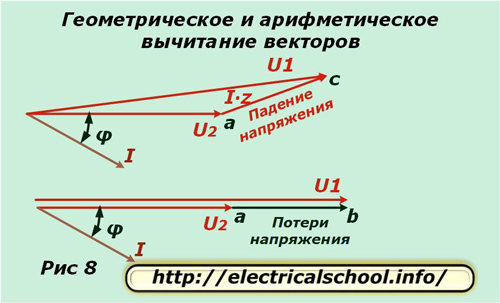
Вывод формул для расчета потери напряжения
Теперь вернемся к рисунку 7 и обратим внимание, что отрезок bd очень маленький. По этой причине при расчетах им пренебрегают, а потери напряжения рассчитывают по длине отрезка ad. Он состоит из двух отрезков ae и ed.
Поскольку ae=I∙R∙cosφ, а ed=I∙x∙sinφ, то потери напряжения для одной фазы можно вычислить по формуле:
∆Uф=I∙R∙cosφ+I∙x∙sinφ
Считая нагрузку симметричной во всех фазах (условно пренебрегая 3I0) можно математическими методами вычислить потери напряжения в линии.
∆Uл=√3I∙(R∙cosφ+x∙sinφ)
Если правую часть этой формулы умножить и разделить на напряжение сети Uн, то получим формулу, позволяющую выполнять расчет потерь напряжения через мощности.
∆Uл=(P∙r+Q∙x)/Uн
Величины активной P и реактивной Q мощностей можно снимать с показаний электросчетчиков линии.
Таким образом, потери напряжения в электрической схеме зависят от:
-
активного и реактивного сопротивления цепи;
-
составляющих приложенной мощности;
-
величины приложенного напряжения.
Вывод формул для расчета поперечной составляющей падения напряжения
Вернемся к рисунку 7. Векторную величину ас можно представить гипотенузой прямоугольного треугольника acd. Катет ad мы уже вычислили. Определим поперечную составляющую cd.
На рисунке видно, что cd=cf-df.
df=ce=I∙R∙sin φ.
cf=I∙x∙cos φ.
cd=I∙x∙cosφ-I∙R∙sinφ.
Используя выведенные закономерности проведем небольшие математические преобразования и получим поперечную составляющую падения напряжения.
δU=√3I∙(x∙cosφ-r∙sinφ)= (P∙x-Q∙r)/Uн.
Определение формулы для расчета напряжения U1 в начале ЛЭП
Зная величину напряжения на конце линии U2, потери ∆Uл и поперечную составляющую падения δU, можно вычислить по теореме Пифагора величину вектора U1. В развернутой форме она имеет следующий вид.
U1=√[(U2+(Pr+Qx)/Uн)2+((Px-Qr)/Uн)2].
Практическое применение
Расчет потерь напряжения выполняется инженерами на стадии создания проекта электрической схемы для оптимального выбора конфигурации сети и составляющих ее элементов.
В процессе эксплуатации электроустановок при необходимости могут периодически проводиться одновременные замеры векторов напряжений на концам линий и сравнение полученных результатов методом простых расчетов. Этот способ актуален для устройств, к которым предъявляются повышенные требования, обусловленные необходимостью высокой точности работы.
Потери напряжения во вторичных цепях
Примером могут служить вторичные цепи измерительных трансформаторов напряжения, которые по длине иногда достигают нескольких сотен метров и передаются специальным силовым кабелем увеличенного сечения.
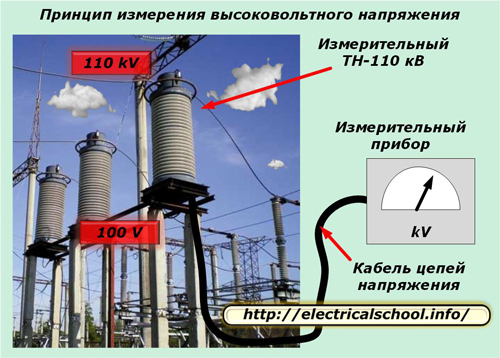
К электрическим характеристикам такого кабеля предъявляются повышенные требования по качеству передачи напряжения.
Современные защиты электротехнических объектов требуют работу измерительных систем с высокими метрологическими показателями и классом точности 0,5 или даже 0,2. Поэтому потери подводимого к ним напряжения необходимо контролировать и учитывать. Иначе вводимая ими погрешность в работу оборудования может существенно влиять на все эксплуатационные характеристики.
Потери напряжения внутри протяженных кабельных линий
Особенность конструкции длинного кабеля состоит в том, что он обладает емкостным сопротивлением за счет довольно близкого расположения токопроводящих жил и тонкого слоя изоляции между ними. Оно дополнительно отклоняет проходящий через кабель вектор тока и изменяет его величину.
Влияние снижения напряжения на емкостном сопротивлении необходимо учесть в расчете для изменения величины I∙z. В остальном описанная выше технология не меняется.
В статье приведены примеры потерь и падения напряжения на воздушных линиях электропередач и кабелях. Однако, они происходят во всех потребителях электроэнергии, включая электродвигатели, трансформаторы, индуктивности, конденсаторные установки и другие устройства.
Величина потерь напряжения для каждого вида электрооборудования законодательно регламентирована применительно к условиям эксплуатации, а принцип их определения во всех электрических схемах действует одинаково.