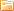Обратная связь - воздействие выходной величины какой-либо системы С (рис. 1) на вход этой же системы. В более широком смысле обратная связь — воздействие результатов функционирования некоторой системы на характер этого функционирования.
На функционирующую систему, кроме выходной величины, могут действовать также внешние воздействия (х на рис. 1). Цепь AB, по которой передается обратная связь, называется цепью, линией или каналом обратной связи.
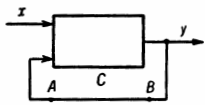
Рис. 1.
Канал может сам содержать какую-либо систему (Д, рис. 2), преобразующую выходную величину в процессе ее передачи. В этом случае говорят, что обратная связь с выхода системы на ее вход осуществляется с помощью или через посредство системы Д.
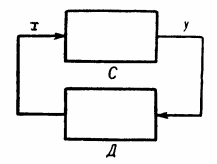
Рис. 2.
Обратная связь является одним из важнейших понятий электроники и теории автоматического управления. Конкретные примеры реализации систем, содержащих обратные связи, можно обнаружить при изучении самых разнообразных процессов в автоматических системах, живых организмах, экономических структурах и т. п.
В силу универсальности понятия применимого в различных областях науки и техники, терминология в этой области не установилась, и в каждой частной области знаний, как правило, используется своя терминология.
Так, например, в системах автоматического регулирования широко применяются понятия отрицательной и положительной обратной связи, которыми определяется связь выхода системы с ее входом через усилительное звено с соответственно отрицательным или положительным коэффициентом усиления.
В теории электронных усилителей смысл этих терминов иной: отрицательной называется обратная связь, уменьшающая абсолютную величину общего коэффициента усиления, а положительной — увеличивающая ее.
В зависимости от способов реализации в теории электронных усилителей выделяют обратные связи по току, по напряжению и комбинированную.
В системы автоматического регулирования часто вводят дополнительные обратные связи, используемые для стабилизации систем или улучшения переходных процессов в них. Они иногда называются корректирующими и среди них выделяют жесткую (осуществляемую с помощью усилительного звена), гибкую (реализуемую дифференцирующим звеном), изодромную и т. п.
В различных системах можно всегда обнаружить замкнутую цепь воздействий. Например, на рис. 2 часть С системы действует на часть Д, а последняя снова на С. Поэтому такие системы называют также системами с замкнутой цепью воздействий, системами с замкнутым циклом или замкнутым контуром.
В сложных системах может существовать множество различных цепей обратных связей. В многоэлементной системе выход каждого элемента может, вообще говоря, воздействовать на входы всех остальных элементов, включая свой собственный вход.
Любое воздействие можно рассматривать с трех основных сторон: метаболической, энергетической и информационной. Первая связана с изменениями расположения, формы и состава вещества, вторая — с передачей и преобразованием энергии, а третья — с передачей и преобразованием информации.
В теории управления рассматривается исключительно информационная сторона воздействий. Таким образом, обратная связь может быть определена как передача информации о выходной величине системы на ее вход либо как поступление информации, преобразованной звеном обратной связи, с выхода на вход системы.
На применении обратной связи основан принцип устройства систем автоматического регулирования (САР). В них наличие обратной связи обеспечивает повышение помехоустойчивости из-за уменьшения влияния помехи (z на рис. 3), действующей в прямом тракте системы.
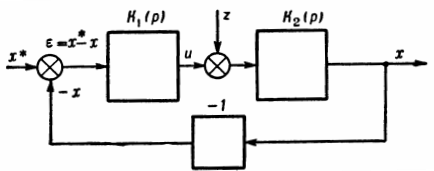
Рис. 3.
Если в линейной системе со звеньями, обладающими передаточными фциями Кх(р) и К2(р), снять цепь обратной связи, то изображение х выходной величины х определится следующим соотношением:

Если при этом требуется, чтобы выходная величина х в точности равнялась задающему воздействию х*, то общий коэффициент усиления системы К(р)= К1(р)К2(р) должен равняться единице, а помеха z должна отсутствовать. Наличие z и отклонение К(р) от единицы обусловливают возникновение погрешности е, т. е. разности
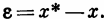
При К(р)=1 имеем
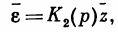
Если теперь замкнуть систему с помощью обратной связи, как показано на рис. 3, изображение выходной величины х будет определяться следующим соотношением:
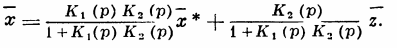
Из соотношения следует, что при достаточно большом по модулю коэффициент усиления Кх(р) второе слагаемое пренебрежимо мало и, следовательно, влияние помехи z ничтожно. В то же время значение выходной величины х будет очень мало отличаться от значения задающего воздействия.
В замкнутой системе с обратной связью удается значительно уменьшить влияние помех по сравнению с разомкнутой системой, т. к. последняя не реагирует на действительное состояние управляемого объекта, «слепа» и «глуха» к изменению этого состояния.
Рассмотрим в качестве примера полет самолета. Если заранее с высокой точностью установить рули самолета так, чтобы он летел в заданном направлении, и жестко закрепить их, то порывы ветра и др. случайные и заранее непредвиденные факторы собьют самолет с нужного курса.
Исправить положение в состоянии только система с обратной связью (автопилот), способная сравнивать заданный курс х* с фактическим х и в зависимости от образовавшегося рассогласования изменять положение рулей.
О системах с обратной связью часто говорят, что они управляются ошибкой е (рассогласованием). Если звено Кх(р) представляет собой усилитель с достаточно большим коэффициентом усиления, то при определенных условиях, наложенных на передаточную функцию К2(р) остальной части тракта, замкнутая система остается устойчивой.
В этом случае погрешность е в установившемся режиме может быть сделана сколь угодно малой. Достаточно ей появиться на входе усилителя Кх(р), чтобы на его выходе образовалось достаточно большое напряжение и, которое автоматически компенсирует помеху и обеспечивает такое значение х, при котором разность e=х*—х была бы достаточно мала. Малейшее нарастание е вызывает несоизмеримо большее нарастание u. Поэтому любая (в практических пределах) помеха z может быть скомпенсирована и притом при сколь угодно малой величине погрешности е, шунтирующую тракт с большим коэффициентом усиления, часто называют глубокой.
Обратная связь в смешанных системах имеет место также и при функционировании сложных систем, состоящих из объектов различной природы, но действующих целенаправленно. Такими являются системы: оператор (человек) и машина, учитель и ученик, лектор и аудитория, человек и обучаемое устройство.
Во всех этих примерах мы имеем дело с замкнутой цепью воздействий. По каналам обратной связи оператор получает информацию о характере функционирования управляемой машины, обучающий — информацию о поведении ученика и о результатах обучения и т. п. Во всех этих случаях в процессе функционирования существенно изменяются как содержание информации, передаваемое по каналам, так и сами каналы.
Андрей Повный